순차 탐색
- 리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법
- 보통 정렬되지 않은 리스트에서 데이터를 찾아야 할 때 사용
- 데이터 정렬 여부와 상관 없이 가장 앞에 있는 원소부터 하나씩 확인
- 시간 복잡도 O(N)
ㄴ 데이터의 개수가 N개일 때 최대 N번의 비교 연산
# 순차 탐색
def sequential_search(n, target, array):
# 각 원소를 하나씩 확인하며
for i in range(n):
# 현재의 원소가 찾고자 하는 원소와 동일한 경우
if array[i] == target:
return i + 1 # 현재의 위치 반환
print("생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.")
input_data = input().split()
n = int(input_data[0]) # 원소의 개수
target = input_data[1] # 찾고자 하는 문자열
print("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.")
array = input().split()
# 순차 탐색 수행 결과 출력
print(sequential_search(n, target, array))
이진 탐색
- 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘
- 탐색 범위를 절반씩 좁혀가며 데이터를 탐색
- 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교
- 시간 복잡도 O(logN)
ㄴ 한 번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어듦.

# 재귀 함수로 구현한 이진 탐색
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid-1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid+1, end)
n, target = list(map(int, input().split()))
array = list(map(int, input().split()))
result = binary_search(array, target, 0, n-1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result+1)# 반복문으로 구현한 이진 탐색
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
end = mid - 1
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
start = mid + 1
return None
n, target = list(map(int, input().split()))
array = list(map(int, input().split()))
result = binary_search(array, target, 0, n-1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result+1)
트리 자료구조
- 노드와 노드의 연결로 표현
- 그래프 자료구조의 일종으로 데이터베이스 시스템이나 파일시스템과 같은 곳에서 많은 양의 데이터를 관리하기 위한 목적으로 사용

- 트리는 부모 노드와 자식 노드의 관계로 표현된다.
- 트리의 최상단 노드를 루트 노드라고 한다.
- 트리의 최하단 노드를 단말 노드라고 한다.
- 트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라 한다.
- 트리는 계층적이고 정렬된 데이터를 다루기에 적합하다.
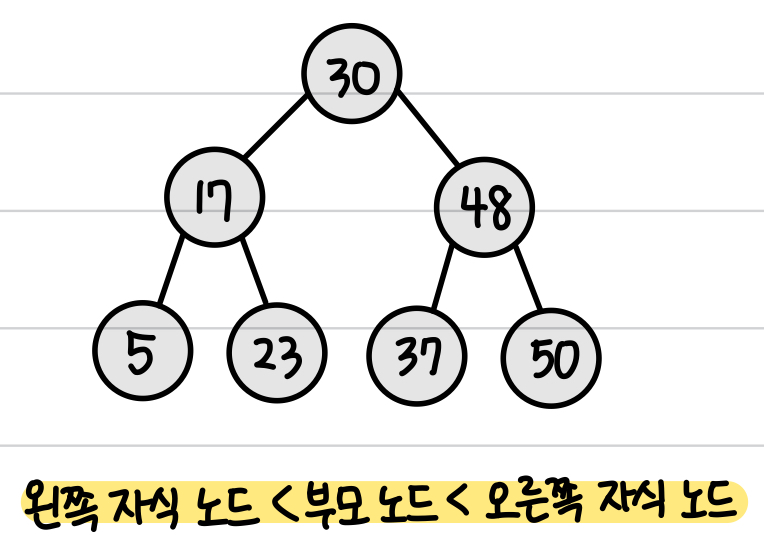
이진 탐색 트리
- 부모 노드보다 왼쪽 자식 노드가 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
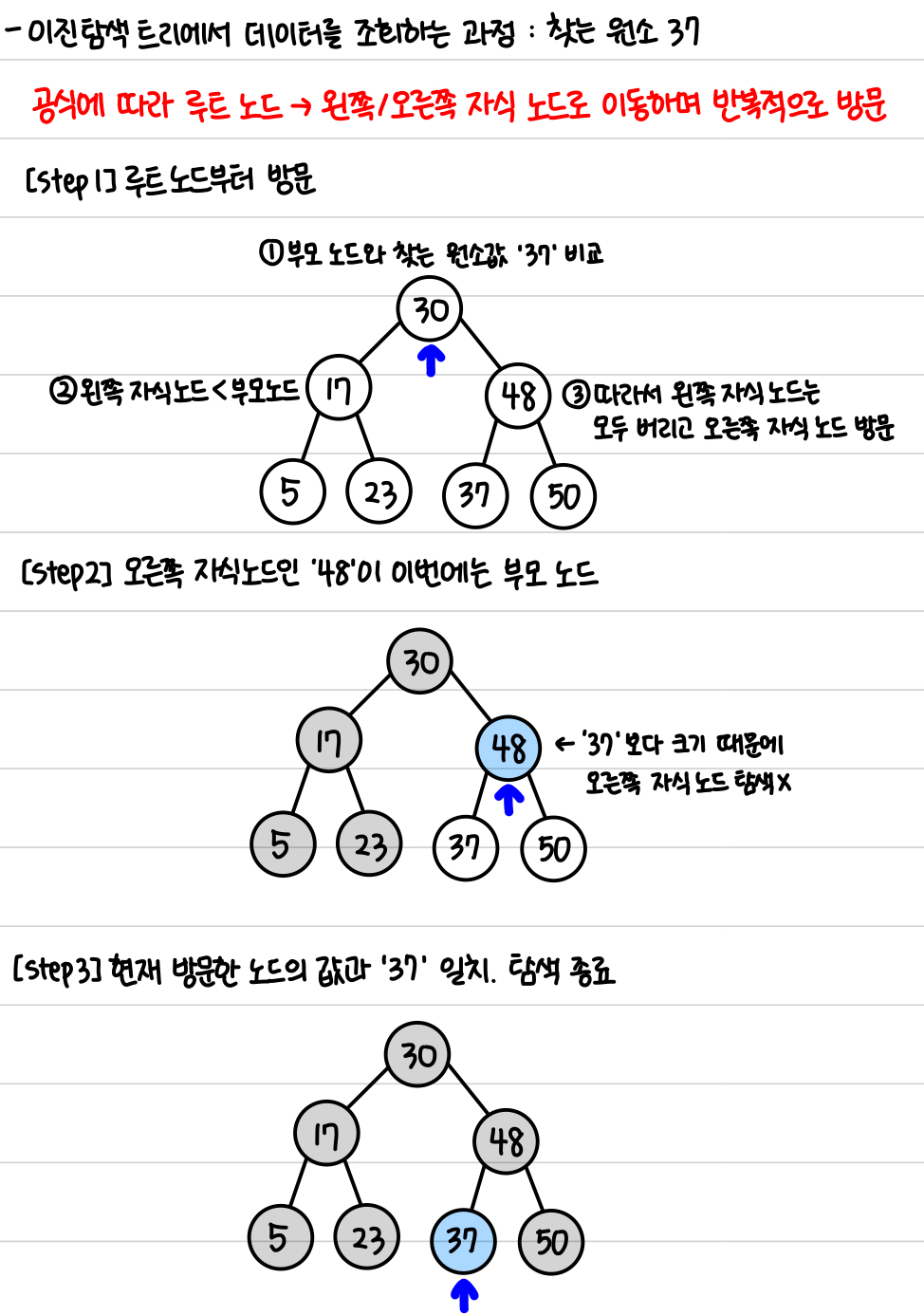
- 이진 탐색 문제는 입력 데이터가 많거나, 탐색 범위가 매우 넓은 편.
- 따라서 sys 라이브러리의 readline() 함수를 이용하자.
실전 문제1. 부품 찾기
1) 내 코드: 이진 탐색을 반복문을 이용해서 풀었음.
# 실전 문제1. 부품 찾기
n = int(input())
n_array = list(map(int, input().split()))
m = int(input())
m_array = list(map(int, input().split()))
n_array.sort()
def binary_search(start, end, target):
while start <= end:
mid = (start + end) // 2
if n_array[mid] == target:
return True
elif n_array[mid] < target:
start = mid + 1
else:
end = mid - 1
return False
for i in m_array:
if binary_search(0, n-1, i):
print('yes', end=' ')
else:
print('no', end=' ')2) 교재 코드
# 실전 문제1. 부품 찾기
# 교재 코드 - 계수 정렬
n = int(input())
array = [0] * 1000001
# 가게에 있는 전체 부품 번호를 입력받아서 기록
for i in input().split():
array[int(i)] = 1
m = int(input())
x = list(map(int, input().split()))
# 손님이 확인 요청한 부품 번호를 하나씩 확인
for i in x:
# 해당 부품이 존재하는지 확인
if array[i] == 1:
print('yes', end=' ')
else:
print('no', end=' ')- 모든 원소의 번호를 포함할 수 있는 크기의 리스트를 만듦.
- 리스트의 인덱스에 직접 접근하여 특정한 번호의 부품이 매장에 존재하는지 확인
# 실전 문제1. 부품 찾기
# 교재 코드 - 집합 자료형 이용
n = int(input())
array = set(map(int, input().split()))
m = int(input())
x = list(map(int, input().split()))
for i in x:
if i in array:
print('yes', end=' ')
else:
print('no', end=' ')- 단순히 특정한 수가 한 번이라도 등장했는지를 검사하면 됨. -> 집합 자료형 이용
실전 문제2. 떡볶이 떡 만들기
# 이진 탐색
# 실전 문제2. 떡볶이 떡 만들기
n, m = map(int, input().split())
array = list(map(int, input().split()))
start = 0
end = max(array)
result = 0
while (start <= end):
total = 0
mid = (start + end) // 2
# 잘랐을 때 떡의 양 계산
for i in array:
if i > mid:
total += i - mid
# 떡의 양이 부족한 경우 더 많이 자르기 (왼쪽 부분 탐색)
if total < m:
end = mid - 1
# 떡의 양이 충분한 경우 덜 자르기 (오른쪽 부분 탐색)
else:
result = mid # 최대한 덜 잘랐을 때가 정답이므로, 여기에서 result에 기록
start = mid + 1
print(result)- 파라메트릭 서치: 최적화 문제를 결정 문제로 바꾸어 해결
- 범위 내에서 조건을 만족하는 가장 큰 값을 찾으라는 최적화 문제라면 이진 탐색으로 결정 문제를 해결하면서 범위를 좁혀갈 수 있다.
- 적절한 높이를 찾을 때까지 절단기의 높이 H를 반복적으로 조정한다.
- 그래서 '현재 이 높이로 자르면 조건을 만족할 수 있는가?'를 확인한 뒤 조건의 만족 여부에 따라 탐색 범위를 좁혀간다.
'🤖 > 알고리즘 정리' 카테고리의 다른 글
| 최단 경로 알고리즘 (Shortest Path Algorithm) (0) | 2022.04.14 |
|---|---|
| 동적 계획법 (Dynamic Programming) (0) | 2022.03.21 |
| 정렬 알고리즘 (Sorting Algorithm) (0) | 2022.02.04 |
| DFS / BFS (깊이우선탐색 / 너비우선탐색) (0) | 2022.01.28 |
| 구현 알고리즘 (Implementation Algorithm) (0) | 2022.01.26 |