투 포인터
리스트에 순차적으로 접근해야 할 때 2개의 점 위치를 기록하면서 처리
특정한 합을 가지는 부분 연속 수열 찾기
* 기본적으로 시작점을 오른쪽으로 이동시키면 항상 합이 감소하고,
끝점을 오른쪽으로 이동시키면 항상 합이 증가하기 때문에
투 포인터 알고리즘으로 해결할 수 있다.
* 리스트 내 원소에 음수 데이터가 포함되어 있는 경우, 투 포인터 알고리즘으로 해결할 수 없다.

n = 5 # 데이터의 개수
m = 5 # 찾고자 하는 부분합
data = [1, 2, 3, 2, 5] # 전체 수열
count = 0
interval_sum = 0
end = 0
# start를 차례대로 증가시키며 반복
for start in range(n):
# end를 가능한 만큼 이동시키기
while interval_sum < m and end < n:
interval_sum += data[end]
end += 1
# 부분합이 m일 때 데이터 증가
if interval_sum == m:
count += 1
interval_sum -= data[start]
print(count)
정렬되어 있는 두 리스트의 합집합
* 시간복잡도 O(N+M) -> 각 리스트의 모든 원소를 한 번씩 순회
* 병합정렬과 같은 일부 알고리즘에서 사용되고 있다.
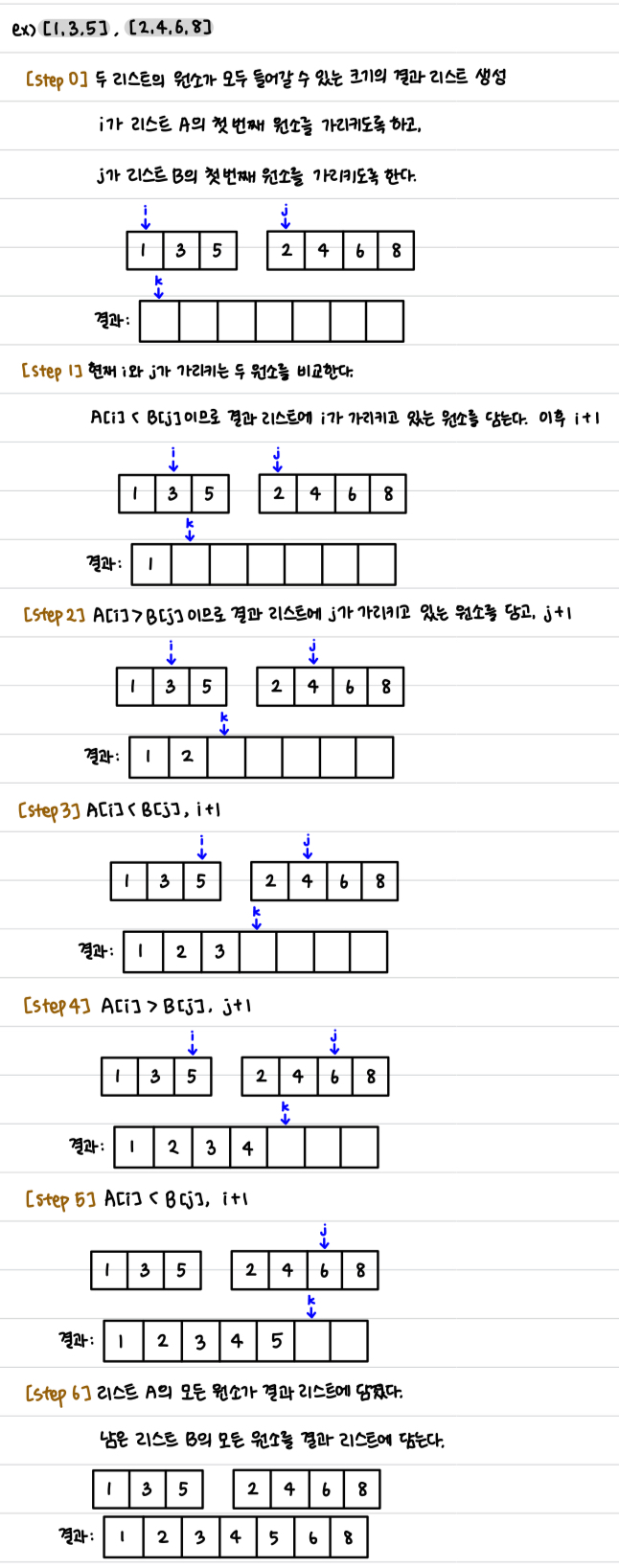
# 사전에 정렬된 리스트 A와 B 선언
n, m = 3, 4
a = [1, 3, 5]
b = [2, 4, 6, 8]
# 리스트 A와 B의 모든 원소를 담을 수 있는 크기의 결과 리스트 초기화
result = [0] * (n+m)
i, j, k = 0, 0, 0
# 모든 원소가 결과 리스트에 담길 때까지 반복
while i < n or j < m:
# 리스트 B의 모든 원소가 처리되었거나, 리스트 A의 원소가 더 작을 때
if j >= m or (i < n and a[i] <= b[j]):
# 리스트 A의 원소를 결과 리스트로 옮기기
result[k] = a[i]
i += 1
# 리스트 A의 모든 원소가 처리되었거나, 리스트 B의 원소가 더 작을 때
else:
# 리스트 B의 원소를 결과 리스트로 옮기기
result[k] = b[j]
j += 1
k += 1
# 결과 리스트 출력
for i in result:
print(i, end=' ')
'🤖 > 알고리즘 정리' 카테고리의 다른 글
| 그래프 이론 (Graph) (0) | 2022.07.18 |
|---|---|
| 최단 경로 알고리즘 (Shortest Path Algorithm) (0) | 2022.04.14 |
| 동적 계획법 (Dynamic Programming) (0) | 2022.03.21 |
| 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2022.02.10 |
| 정렬 알고리즘 (Sorting Algorithm) (0) | 2022.02.04 |